Revisiting the Dependence of Poisson’s Ratio on Liquid Fragility and Atomic Packing Density in Oxide Glasses
0
Poisson’s ratio (ν) is the negative ratio of the transverse strain to the longitudinal strain of a material under uniaxial stress in the elastic regime. It relates to the shear modulus (G) and bulk modulus (B), as
For isotropic materials in three dimensions, this limits ν to be within −1 and 0.5, as the values of G and B are always positive. Different material families and compositions exhibit pronounced diversity in their elastic properties and thus Poisson’s ratio. Materials with ν ~ 0.5 are highly incompressible and tend to deform through shape change, while materials with ν ~ 0 are highly compressible. So-called auxetic materials, with negative values of ν, swell under tension. At ν ~ 0.2, a transition between two different types of stress patterns in frozen-in solid has been reported, namely shear and uniform deformation. Various macroscopic properties have been linked to Poisson’s ratio, including some outside the elastic regime, such as densification, connectivity, and ductility.
Oxide glasses exhibit interesting properties such as transparency, high hardness, high chemical durability (in many cases), and low-cost of raw materials. The brittleness of oxide glasses has been a major hindrance for their use in various engineering and functional applications. As the crack tip formation and growth mechanisms are not well understood, it is challenging to design ductile oxide glasses. Post-processing approaches such as chemical strengthening are thus currently used to improve the mechanical performance. However, molecular dynamics (MD) simulations suggest that silicate glasses can exhibit some nanoscale ductility, and it is also possible for silica glass to feature ductility induced by electron-beam irradiation. Interestingly, as shown for metals and metallic glasses, high G/B ratio (and thus low Poisson’s ratio) favors brittleness. In other words, a correlation between fracture energy (Gfrac), i.e., energy required to create two new fracture surfaces, and Poisson’s ratio has been observed, which also manifests itself by a brittle-to-ductile (BTD) transition around νBTD = 0.32 not only for metallic glasses but various non-crystalline solids.
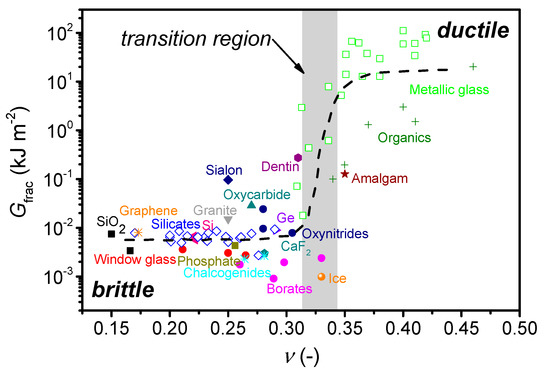
Figure 1. Dependence of fracture energy (Gfrac) on Poisson’s ratio (ν) for a range of materials, showing a brittle-to-ductile transition in the range of ν from 0.30 to 0.33. The figure is reproduced with the data from Lewandowski et al. and Tian et al. We also extend it with new Gfrac data for silicate glasses, borate, chalcogenide, and metallic glasses, and graphene obtained by single-edge pre-crack beam (SEPB), chevron notch (CN), single edge notch beam (SENB), indentation fracture (IF), or tensile testing methods. The error of ν and Gfrac is estimated to be 0.01 and 15%, respectively. The dashed line is a guide for the eye.
The problem for oxide glasses is the fact that they mostly exhibit ν < 0.30, with only few oxide glasses reported with ν > 0.34. As such, the existence of a BTD transition for oxide glasses needs additional verification. However, recent MD simulations on permanently densified SiO2 glasses have confirmed the existence of a BTD transition, although the value of νBTD was found to depend on the average coordination number. Moreover, a recent study has explained the empirical BTD transition based on microscopic dynamical properties, building on the observation that ductility is closely related to the secondary β-relaxation, while Poisson’s ratio is proposed to be related to the effective Debye-Waller factor. The study suggests that ductile materials can withstand deformation at higher rates because they exhibit faster β-relaxation.
In an attempt to overcome the brittleness of oxide glasses, it is thus of great interest to discover high-ν oxide glasses (ν > 0.32). Unfortunately, there are presently no composition-dependent models available for predicting ν, and thus, inefficient Edisonian trial-and-error composition design is currently utilized. It is therefore of interest to find predictable surrogates for Poisson’s ratio. Most notably, liquid fragility (m) has been proposed to be positively correlated with the ratio of bulk and shear moduli (and thus Poisson’s ratio) for a broad range of glassy systems covering covalent and hydrogen-bonded, van der Waals and ionic glasses, i.e., a range of organic molecules, oxide, halogenide, and chalcogenide glasses. Angell’s liquid fragility is defined as the slope of the base-10 logarithm of viscosity versus Tg-scaled inverse temperature curve at Tg, where Tg is the glass transition temperature (m = d log (η)/d log (Tg/T) at Tg). This is the fragility index used in this work, although we note that other definitions of fragility exist. The proposed m-ν relation is of interest, since tools such as topological constraint theory and coarse-graining (related to structural connectivity) can be used to predict m. Since the original study by Novikov and Sokolov in 2004, a similar m-ν dependence has been found for metallic glasses, although the change in fragility with modulus ratio varies for different systems. It has been noted that the correlation is only observed within a narrow range of mdue to the limited amount of data on bulk metallic glasses. The proposed linear relationship between m and the bulk-to-shear modulus has been seriously questioned by Yannopoulos and Johari, who have argued that some data points were erroneously plotted, showing that no general correlation for neither organic, inorganic, nor metallic glasses exists when including more data. The lack of correlation between m and elastic properties has then been suggested to be due to the strong sensitivity of ν to temperatures above Tg, as strong melts (low m) exhibit Poisson’s ratio that is almost constant before and after the glass transition, while fragile melts (high m) show a significant change in Poisson’s ratio above Tg. There have been studies supporting the m-ν correlation. For example, building on a proposed relation between Poisson’s ratio and packing density (see below) Duval et al. argue that the relation between m and ν is due to the structural fluctuations being breathing-like (with change of volume) in strong liquids and shear-like (without change of volume) in fragile liquids. Greaves et al. have also argued that the correlation between m and ν depend on the glass system, showing linear correlations for binary alkali silicates and metallic glasses, but with different slopes.
Besides liquid fragility, Poisson’s ratio has been suggested to be positively correlated with the atomic packing density (Cg), which is defined as the ratio between the volume occupied by the ions and the corresponding effective volume of glass. Cg could potentially be a good surrogate for Poisson’s ratio, since the compactness of the sample affects the vibrational modes and materials with a high Cg should exhibit relatively strong interatomic interactions. Based on experimental data, an empirical relation between ν and Cg has been proposed (ν = 0.5–1/7.2Cg), but it has been found to overestimate the Poisson’s ratio for borate and phosphate glasses and underestimate it for germanate and aluminate glasses. A reason for an overestimated Poisson’s ratio of borate glasses might be the low average coordination number as explained for the prediction of Young’s modulus.
The purpose of this work is to revisit the validity and universality of the proposed m-νand Cg-ν correlations. This is done to determine whether prediction of liquid fragility or atomic packing density can be used to guide the discovery of oxide glasses with high Poisson’s ratio (ν > 0.32), which are expected to be ductile following the relation in Figure 1. To do so, we perform an extensive literature review to obtain liquid fragility, density, and Poisson’s ratio data for various glass systems. Since experimental data on oxide glasses with ν > 0.30 are scarce, we also synthesize a total of 20 new oxide glasses, particularly aluminoborate and zinc borate glasses as these have been found to have relatively high Poisson’s ratio. To further expand the dataset, we also determine the missing property (e.g., m if only Cg and ν are known) from previously synthesized glasses in our laboratory. Moreover, we subject selected oxide glasses to high-temperature densification to induce a higher Cg value in bulk samples and then probe whether it correlates with an expected increase in ν. Finally, we also discuss the implications of the findings for designing tough oxide glasses.